
출처 : https://www.acmicpc.net/problem/1003
아이디어
해당 문제는 대표적인 그래프 탐색 유형의 문제이며, '중복 연산'에 대한 핵심 인사이트를 개념으로 설명하는 문제이다. 다만, 피보나치 값을 물어보는 것이 아닌, 단말노드인 0과 1을 몇 번 탐색하느냐를 요구사항으로 제시한다.
먼저, 일반적인 피보나치 수열에 대한 그래프와 이에 따른 0과 1 단말노드 관점을 시각화하여 살펴보자.
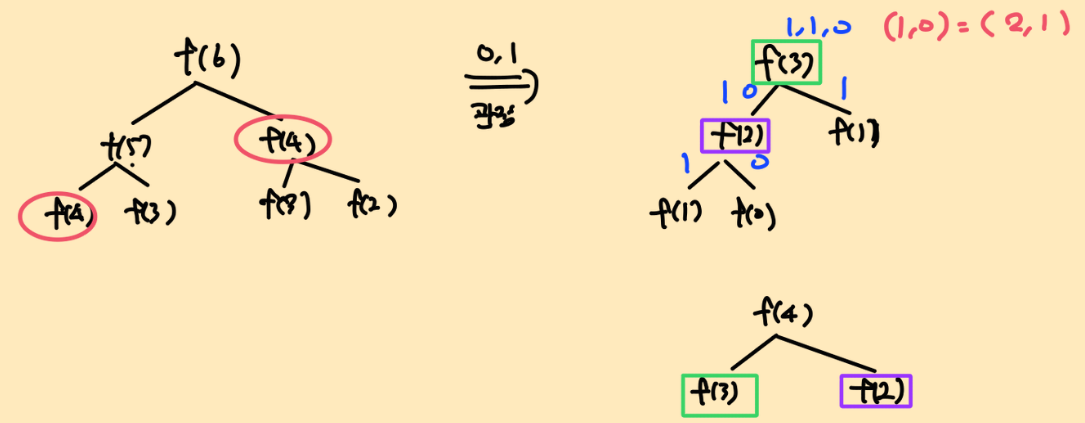
왼쪽 그래프에서 Fibo(4), Fibo(3), Fibo(2)과 중복으로 연산된다는 사실을 알 수 있으며, 다음의 DP 조건을 만족하므로, 알고리즘으로 DP를 선택할 수 있다.
- 큰 문제를 작은 문제로 나눌 수 있는가
- 작은 문제의 답이 큰 문제에서 일부분으로 사용되는가
- 이 과정에서 중복되는 연산이 있는가
즉, 원래 피보나치 수열의 값을 물어보는 DP문제에서 기존 dp테이블은 다음과 같이 설정했었다.
- DP[x]=value : x 피보나치 수열의 value값
- ex) DP[3]=DP[2]+DP[1]=2
사진에서 오른쪽 그래프(0,1 관점)을 살펴보게 되면, 왼쪽 그래프처럼 서브트리에서 0과 1을 전달하는 모습을 알 수 있다. 다시 말해, 재귀라는 특성은 동일하며 중복 연산의 관점이 값을 전달하는 것에서 0과 1의 개수를 전달하는 것으로 살짝 변경된 것 뿐이다. 이를 바탕으로, DP 테이블을 다음과 같이 살짝 변경하면 된다.
- DP[x]=[zero_count, one_count] : x 피보나치 수열의 [사용된 0의 개수, 사용된 1의 개수] 값 (즉 2차원 배열)
- ex) DP[3] = [1,2] : Fibo(3)은 1개의 0, 2개의 1이 사용되었다.
그러므로, 이러한 DP 설정을 바탕으로 TOP-DOWN(DFS+Memozation) 또는 Bottom-UP(for문)으로 프로그램을 구현하면 된다. 필자는 모두 구현해보았으므로, 정답 코드에서 자세한 코드를 확인 가능하다.
정답 코드
TOP-DOWN
### TOP-DOWN
input=__import__('sys').stdin.readline
def dfs(x):
if x==0: # 단말 노드 0 도달 시
dp[0]=[1,0]
return dp[x]
if x==1: # 단말 노드 1 도달 시
dp[1]=[0,1]
return dp[x]
if dp[x]!=[0,0]: # 기존에 연산했던 x라면.(중복 연산 체크)
return dp[x]
left=dfs(x-1) # 왼쪽 서브트리의 0 및 1 개수 리턴
right=dfs(x-2) # 오른쪽 서브트리의 0 및 1 개수 리턴
dp[x][0]+=left[0]+right[0]
dp[x][1]+=left[1]+right[1]
return dp[x]
for _ in range(int(input())):
n=int(input())
dp=[[0,0] for _ in range(n+1)]
dfs(n)
print(*dp[n])BOTTOM-UP
### Bottom-UP
input=__import__('sys').stdin.readline
for _ in range(int(input())):
n=int(input())
if n in [0,1]: # 피보나치 수열 0과 1을 물어보면
print(*'1001'[n::2]) # 바로 출력
continue
# n이 2이상이면
dp=[[0,0] for _ in range(n+1)]
dp[0],dp[1]=[1,0],[0,1]
# 작은 문제에서 부터 차근차근 개수들을 저장
for x in range(2,n+1):
dp[x][0]=dp[x-1][0]+dp[x-2][0]
dp[x][1]=dp[x-1][1]+dp[x-2][1]
print(*dp[n])
'Problem Solving > Baekjoon' 카테고리의 다른 글
| [백준] 16120 : PPAP (Python) (0) | 2025.01.24 |
|---|---|
| [백준] 2343 : 기타 레슨 (Python) (0) | 2025.01.22 |
| [백준] 1068 : 트리 (Python) (1) | 2025.01.20 |
| [백준] 14271 : 그리드 게임 (Python) (2) | 2025.01.19 |
| [백준] 28107 : 회전초밥 (Python) (0) | 2025.01.18 |
