
출처 : https://www.acmicpc.net/problem/12869

아이디어
'한 번에 3개의 scv를 공격할 수 있다.'
해당 요구사항을 바탕으로, '어떤 scv에 제일 높은 공격을 진행할 것인가'에 대한 인사이트가 이번 문제의 핵심이다. scv수가 3개인 상황을 예시로 경우의 수가 어떻게 나뉘는지 살펴보자.
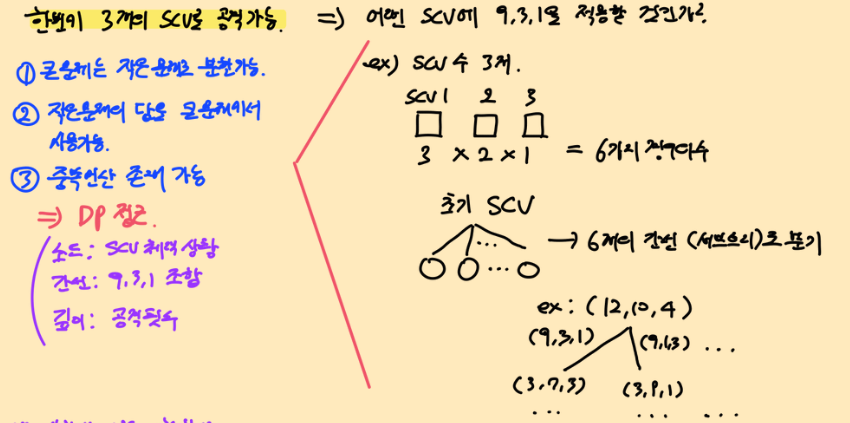
먼저, 3개의 scv를 공격하는 방법은 순열이라는 것을 알 수 있다. 즉, 6가지 경우의 수가 존재한다는 것이고, 이는 그래프 상에서 분기되는 간선(자식 서브트리)에 해당된다.
이러한 그래프와 scv 공격과의 관계를 바탕으로 다음과 같은 해석을 진행할 수 있다.
- 큰 문제(초기 scv의 공격 최소 횟수)는 작은 문제(서브트리의 scv의 공격 최소 횟수)로 분할 가능하다.
- 작은 문제의 답을 큰 문제에서 사용할 수 있다.
- 중복 연산이 존재할 수 있다.
이는 DP의 조건과 부합하므로, DP로 접근할 수 있다.
상향식(Bottom-Up)
'scv의 체력이 0 또는 그 이하가 되면...'
해당 요구사항을 통해 scv의 체력이 음수이면 0으로 치환이 가능하다는 사실을 알 수 있고, 이를 통해 DP 테이블의 초기값 설정을 진행할 수 있다.
그러나, DP테이블의 차원이 현재 문제에서는 변동적(유동적)이다. 그 이유는 scv의 개수 입력이 1부터 3까지로 가변적이기 때문이다. 예를 들어, n=2라면 dp[scv1][scv2]가 되고, n=1라면 dp[scv] 된다.
그러므로, 필자는 DP 테이블을 딕셔너리로 설정하여, 딕셔너리의 key를 튜플로 접근하는 방식을 고안하였고, 이를 후술할 하향식(Top-Down)으로 설계 및 구현하였다.
하향식(Top-Down)
위의 사진에서 예제 그래프를 보면 알 수 있듯이, 공격받은 경우를 나타내는 각 서브트리들을 재귀를 통해 접근하는 방식이다. 그래프의 정의를 다음과 같이 표현할 수 있다.
- 노드 : scv의 체력 상황
- 간선 : 9,3,1 조합(순열)
- 깊이 : 공격횟수
이러한 그래프 정의를 통해, 중복 연산을 위한 DP테이블은 다음과 같이 설정한다.
- DP테이블 : {}
- ex) DP[(12,10,4)]=2 : (12,10,4)의 체력을 갖는 scv들은 최소 2번 공격하면 파괴가 가능하다.
재귀를 통해 작은 문제로 접근하고, 최소값이 저장된 작은 문제들의 답을 큰 문제에서 이용하도록 코드를 구현하면 된다.
정답 코드
# https://www.acmicpc.net/problem/12869
# 뮤탈리스크
# dp,그래프탐색
# Top-Down (성공)
input=__import__('sys').stdin.readline
# scv개수 3일때의 탐색
def dfs_n_3(s1,s2,s3,cnt):
# scv들의 체력이 모두 0이하라면
if s1<=0 and s2<=0 and s3<=0:
try: # 기존의 공격 방식보다 더 적은 공격 방식 저장.
dp[(0,0,0)]=min(dp[(0,0,0)],cnt)
except: # 해당 공격 방식을 처음 탐색한 경우
dp[(0,0,0)]=cnt
return dp[(0,0,0)] # 부모에게 공격횟수 전달
# 해당 scv 체력에서의 공격 경우를 이미 탐색한 경우
if (s1,s2,s3) in dp.keys():
return dp[(s1,s2,s3)] # 부모에게 해당 공격 횟수 전달
# 해당 scv의 공격을 처음하는 경우
# 공격 경우의 수 탐색
for i,j,k in [(9,3,1),(9,1,3),(3,9,1),(3,1,9),(1,9,3),(1,3,9)]:
dp[(s1,s2,s3)]=dfs_n_3(s1-i,s2-j,s3-k,cnt+1) # 자식 서브트리의 공격횟수 전달받기
return dp[(s1,s2,s3)] # 최종적인 공격 횟수 리턴
def dfs_n_2(s1,s2,cnt):
if s1<=0 and s2<=0:
try:
dp[(0,0)]=min(dp[(0,0)],cnt)
except:
dp[(0,0)]=cnt
return dp[(0,0)]
if (s1,s2) in dp.keys():
return dp[(s1,s2)]
for i,j in [(9,3),(9,1),(3,9),(3,1),(1,9),(1,3)]:
dp[(s1,s2)]=dfs_n_2(s1-i,s2-j,cnt+1)
return dp[(s1,s2)]
def dfs_n_1(s,cnt):
if s<=0:
try:
dp[0]=min(dp[0],cnt)
except:
dp[0]=cnt
return dp[0]
if s in dp.keys():
return dp[s]
for i in [9,3,1]:
dp[s]=dfs_n_1(s-i,cnt+1)
return dp[s]
n=int(input())
scvs=[*map(int,input().split())]
dp={}
if n==3:
print(dfs_n_3(scvs[0],scvs[1],scvs[2],0))
elif n==2:
print(dfs_n_2(scvs[0],scvs[1],0))
else:
print(dfs_n_1(scvs[0],0))
'Problem Solving > Baekjoon' 카테고리의 다른 글
| [백준] 2800 : 괄호 제거 (Python) (0) | 2025.02.07 |
|---|---|
| [백준] 2579 : 계단 오르기 (Python) (2) | 2025.02.06 |
| [백준] 13904 : 과제 (Python) (1) | 2025.02.01 |
| [백준] 1072 : 게임 (Python) (0) | 2025.01.30 |
| [백준] 11726 : 2 x n 타일링 (Python) (1) | 2025.01.29 |
